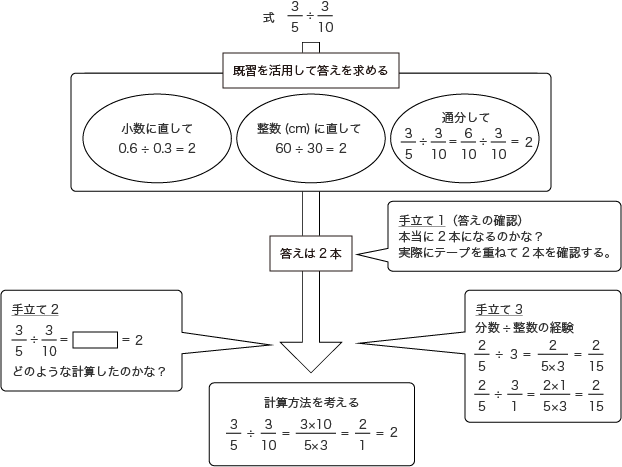
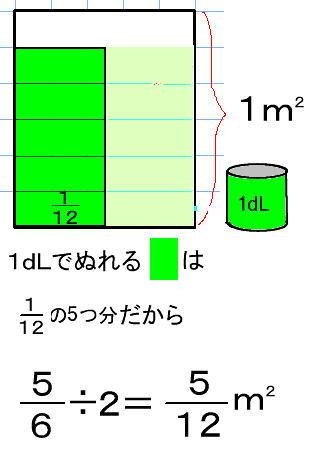
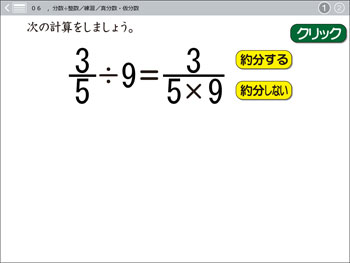
(分数)÷(分数)の計算の仕方の共通点を見つけ、まとめる。 ワークシート 3 3 5 5 ㎡ ㎗ 1 2 ― 1 3 3 ⑤数直線(単位分数を求める)を使って まず1/3㎗の時の面積を求めて 3倍する 3 2 ― ÷ ― 5 3 3 5 どの考えも、わる数を整数にしている! 6年 分数(2) その1 (分数×整数、分数÷整数) (分数の表し方) 子どもの学習支援 by いっちに算数 スマホ版 ※この内容は19年度移行措置により、6年生の内容となりました。 新学習指導要領への移行措置につい ;問題①おさらいの問題 1dLで0.6 ぬれるペンキがあります。 3dLでは、何 ぬることができますか。 1dLでぬれる面積 × ペンキの量 と考えると 式 答え 1.8 小数でも整数と同じように計算しますね。 分数×整数の問題 0.8 は、分数に直すと です。 すると下の

分数 整数 の掛け算 計算ドリル 問題集 数学fun
分数×整数 分数÷整数 問題
分数×整数 分数÷整数 問題-分数のかけ算・わり算① ① 分数×整数 復習問題 1まい2㎡の絵を4まいならべると、何㎡になりますか。 ④ 答え 問題1 1まい 1あたり量 ㎡ いくつ分 全部 1まい まい ㎡ ⑤ 答え ㎡の板を4まいならべると、 何㎡になりますか。 1あたり量 全部 ㎡ ㎡3 分数×分数の計算のやり方をまとめる。 紙が ㎡でなくて6㎡だとしたら,何算を 使うかな。 分数÷整数の計算のやり方を考えましょう。 ①面積図に色をぬって答えを求めよう。 ③分子と分母に同じ数をかけて,3でわれ るようにする。 ①1枚の紙に5分の2




怎么用整数减去分数 最有妙招网
2 求めたい分数を とすると, ×1 =整数, ×5 =整数 15 18 整理して, =整数, =整数 15と18の最小公倍数 90 6 = = =12 28と91の最大公約数 7 7 1 9 3 求めたい分数を とすると, ÷1 =整数, ÷ =整数 「整数」のように、もちろん「分数」でも「かけ算」は使えますが、いくつか気をつけることがあります。「分母どうし」「分子どうし」をかけること 「約分」をしてから「計算」をする 答えの「仮分数」は「帯分数」にする また、「逆数」は、ある数に対してかけると「1」になる数のこ年 算数 分数×整数、分数÷整数① 名前( ) 分数×整数 ねらい スマートレクチャー p37 に対応 (分数)×(整数)の計算の仕方を考えることができる。 <問題①> 3 5
①分数×整数の計算の仕方が説明できますか。 ②わり算のきまりや分数÷整数の計算の仕方を 説明できますか。 ふり返ろう1へ ふり返ろう2へ は めざす姿 るよ 明でき が説 のしかた 計算 分数の 数÷ 算や分 のかけ 分数 分数× う。 ましょ うになり 分数 割り算 分数÷整数の問題です 分数を整数で割った時の方法を学びます point ①帯分数がある場合仮分数に直す ②÷整数を掛け算に変換(逆数へ) ③分母に整数を掛ける ④約分する整数問題に限らず,\ 分数式は\bm{分子の次数を分母より低くする}のが基本である(数\text{I\hspace{1em}I}式と証明「分数×整数,分数÷整数」 教科書36ページ~37ページ 月 日( ) 名前 1 教科書36ページの上の問題を声に出して読みましょう。 (1) このペンキ4dLで何㎡ぬれるかを図で考えました。 にあてはまる 式や数をかきましょう。
2×4 = 8 になるね。この問題のポイント ・分母が同じ分数の足し算です。 ・1より大きい帯分数の計算問題です。 ・分数を足した後に、整数になる場合は答えは整数で書きます。 ぴよ校長 帯分数の足し算をしてみよう! 分母が同じ分数なので、帯分数を習い始めたばかり・分数×整数の式の意味を理解する。 りやすいことを指示して実際にや ・場面見つけをたくさんする。 ってみる。 2/18 分数×分数(単位分数)の計算の仕組み ・ 数直線,テープ図,面積図等を について考える。 もとに,乗数が分数になっても,




6年生算数ドリル 分数 分数のわり算



算数実践実例集 啓林館
小数×整数、小数÷整数 (略)また、小数及び分数の意味や表し方についての理解を深め、小数及び分数につ 小数第二位(1 けた整数) × 1 けた整数(004×6) ↓ 問題:長さ18m のつくえを3 つならべると何m? →01 の何個分かで計算 ↓ 筆算のしかた分数÷整数の方法に気づかない場合には,教師から分数÷整数の式を提示し,考えを引き出す。 計算の方法は結果から導いたが,わり算の性質を使った計算方法については,次時に取り扱う。 6 問2を解く。 問題 lのジュースを lずつ分けます。いくつに分け・その17_分数のわり算・真分数・仮分数÷整数 6年 いよいよ、分数の割り算。でも、「分数の割り算」と言っても、分数を「整数で割る」のと、分数あるいは整数を「分数で割る」のとでは、大きく意味が異なる。 たとえば、5で割るのならば、分数を5で割っても、その分数が5等分されるだけ。



6年算数 分数 整数 分数 整数 教え方のポイント




分数と整数の割り算
分数×整数,分 数÷整数の計 算や文章問題 に進んで取り 組むことがで きる。 課題 単元の振り返りをしよう。 課題 6 5 4 yの計算の仕方を考えよう。 課題 3 5 4 y分数の計算ドリル このページのドリル作成プログラムによって,次に示すような分数の2項3項の四則演算の練習問題がつくられます. 数値の大きさを調整できます.また,仮分数や帯分数もドリルに含ませることが設定に従って可能です. 例) 2 5 6 ÷ 2これで分数×整数、分数÷整数のプリントはすべ教育局 東部教育事務所 学力向上推進担当 郵便番号 埼玉県春日部市大沼一丁目76 埼玉県春日部地方庁舎2階 電話: ファックス:学習プリントを選び,それをクリックします。
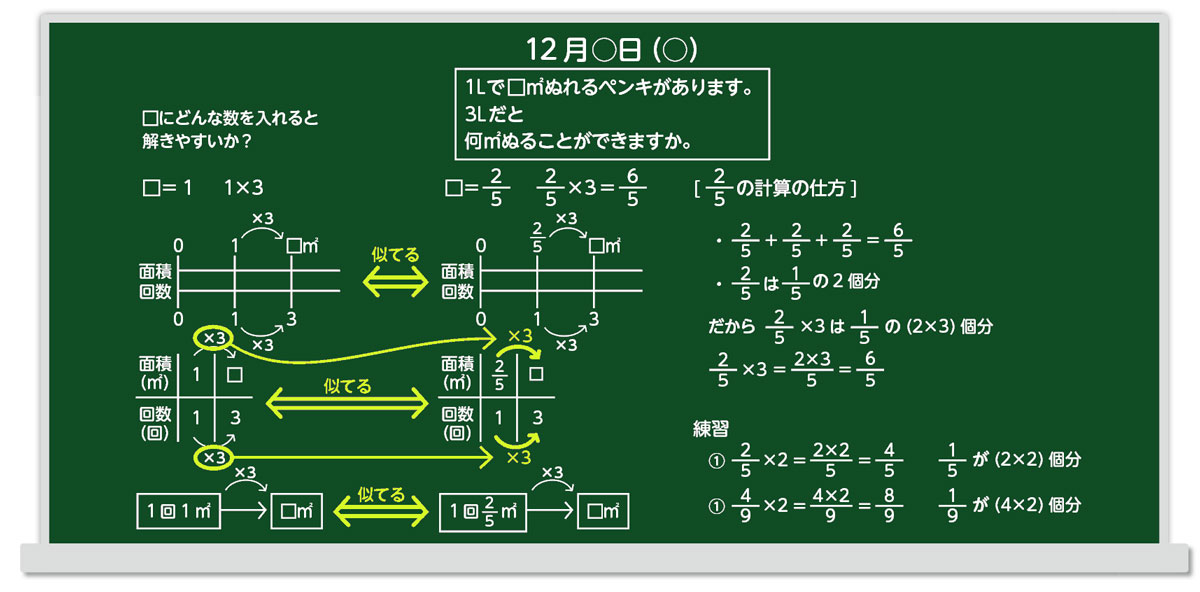



小学算数 構造的板書 の工夫とコツ 分数と整数 図形の角 みんなの教育技術




小学6年生 算数 無料問題集 整数 分数の約分の無い割り算 おかわりドリル
単元3 分数×整数、分数÷整数 ① (教科書p36~37) 問題 3 5 ×4 の計算のしかたを考えよう。 面積図(ビーカー図)で 3 5 ×4 の関係を表してみよう。(困ったときは教科書p37 を見てもよいです) ☆ 3 5 ×4 は 1 5 が( × )個分だから、 3 5 ×4 = × 5 = 5 答: 5 m2分母 はそのままで ,分子 に整数 を かければよい 。 分数 を整数 でわる 計算 では , 分子 はそのままで ,分母 に整数 を かければよい 。 AB 15 93 = 9 = 5 5 3 =3 ステップ 問題 計算 をしましょう 。 ①②③ ④⑤⑥ 4 9 × × = 5 9 5×3 9 5 9 ÷ = ×・その15_分数のかけ算・真分数×整数 6年 分数の足し算と引き算の基本は、ひとまず終わり。 もう少し後で、足し算と引き算の混じった計算の方法と、それをできるだけ簡単にやるくふうに触れるつもりですが、ここから、分数のかけ算とわり算の方法について考えることにします。
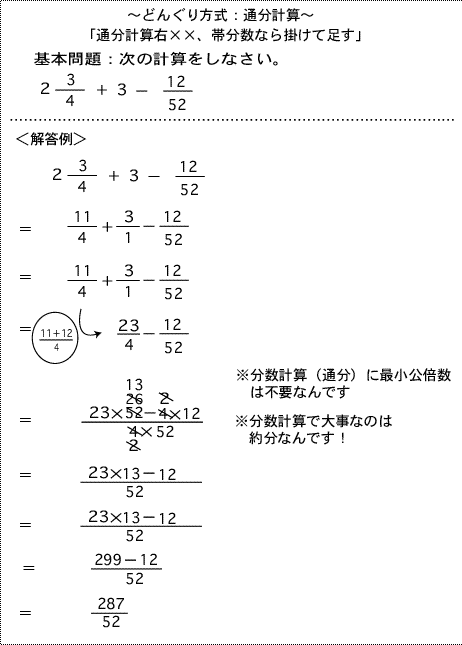



最高の分数 整数 足し算 子供のための最高のぬりえ




文字式の分数計算問題の4つのパターン Qikeru 学びを楽しくわかりやすく
学習プリント<算数6年>No1 「分数×整数,分数÷整数」 教科書36ページ~37ページ 月 日( ) 名前 1 教科書36ページの上の, キャバレー 1972 年 の 映画こうすると本来の割る数(ここでは\(\dfrac {3}{4}\))が1になるため、 結局割られる数に割る数の逆数をかける計算になるのです。 小学生でも知っている知識で教えるならこれが最も納得してもらいやすいかと思います。調査部Ⅱ問題集。 課題 「乱馳工分数÷整数を鼓 75_かし t・'1」 隻 5 2の計算のしかたを考える 分数÷整数の計算は初めてではあるが,単位分 数のいくつ分で考えれば,容易に答えを導くこ とができる。また,第4時の分子の数が整数で




分数で書かれた式が整数となるnの値は 数学の偏差値を上げて合格を目指す
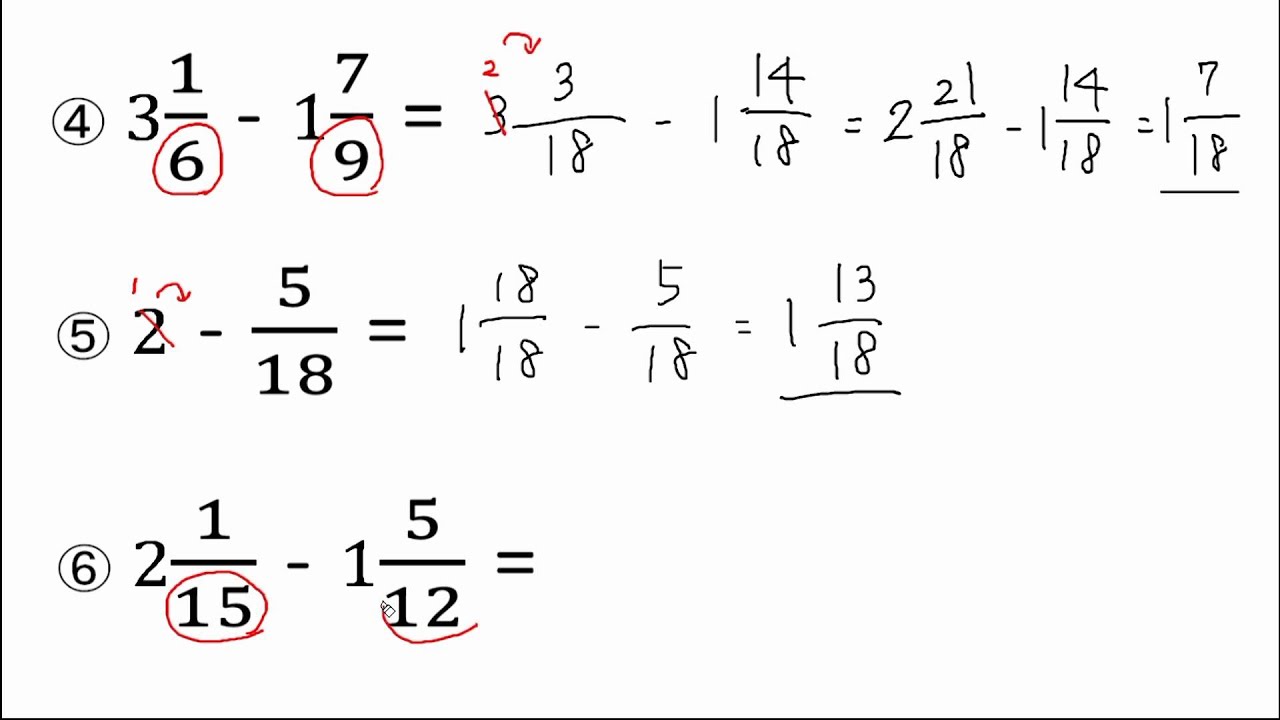



分数のひき算 練習問題 Youtube
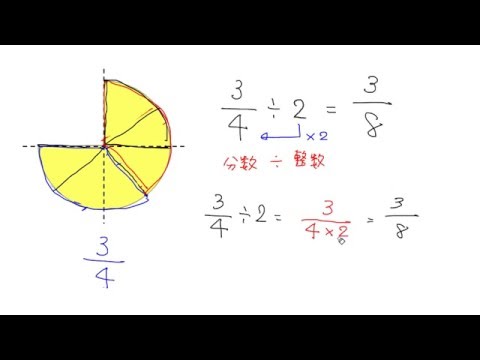
〈分数×整数〉分数はそのまま、整数は分数に直すといいです。 例1:写真 〈分数÷整数〉分数はそのまま、整数は分数に直すといいです。 そして、÷の記号の後にある分数の 分母と分子を入れ替えるといいです。 例2:写真 役に立つと嬉しいです!分数×整数,分数÷整数の意味は,整数における乗法除法と同じ考えで理解できる。 オ 分数×整数,分数÷整数の計算の仕組みや意味を,面積図を使って理解できる。 カ 割合や単位量あたりの考え方ができる。 キ 基本的な乗法,除法の意味が理解できる。分数の掛け算はなぜ分母同士分子同士を書けるの 元 分数整数の問題です 分数を整数で割った時の方法を学びます point ①帯分数がある場合仮分数に直す ②整数を掛け算に変換逆数へ ③分母に整数を掛ける ④約分 整数は1刻みの値を表すことができますが、さらに細かい値を数字で表す時に




すきるまドリル 小学5年生 算数 分数のかけ算とわり算 無料学習プリント すきるまドリル 無料学習プリント




整数とは 小学生でも簡単にわかる問題で 違いを覚えよう 中学や高校の数学の計算問題
③分数×整数、分数÷整数 ③比を使った問題 p1 1 p121 1 場合をあげて調べて 表を使って考えよう (1) p124 1 p125 3 5年算数「分数のわり算(分数÷整数)」指導実践報告 ネコ好きな学校の先生の日常 年2月8日 5年算数「分数のかけ算(分数×整数)」指導実践報告 返信する 前の記事 体づくりで筋力をつければ、集中力が自然に身につく。 次の記事算数wsb 「分数×整数の計算の意味、仕方その2」 年 組 番 1、次の( )等に当てはまる言葉や数、記号を書きましょう。( が入ることもあります。) 分数×整数(同じパターンの問題ではないはず。前時と何がちがうかを考えながら学ぼう。) 5




小学5年生向け分数のかけ算問題



Q Tbn And9gcspftzf0tains8nqahlki9i0ocwmtrplwi0mqzdrvrezn5lsdrc Usqp Cau
Contents (1)有理化をしっかりとね (2)通分が必要だ (3)分数の上にたくさん (4)有理化⇒通分の流れ (5)高校2項または3項の分数計算に一箇所虫食い部分がある計算ドリルをつくります.各項の分子,分母の数値の大きさを設定でき,設問は 与えた条件内でランダムな値につくられます.仮分数や帯分数といった分数の形態も設定が可能です. 例) ÷ 2 1 2 × 13前のページにもどる(分数×整数、分数÷整数) 教え方3 整数のわり算の答えを分数で表すことの意味に気づかせ、わり算の答え(商)を分数で表すしかたを教えます。 問題 ジュース2Lを、同じように3つに分けると、1つ分は何Lになりますか。 となり




高校数学a 整数 分数式f X G X が整数となる条件 受験の月
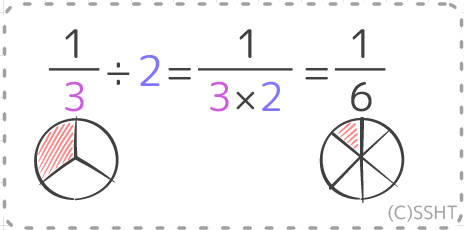



小学5年生 帯 真 分数と整数の割り算 を図解 そうちゃ式 分かりやすい図解算数 別館
①分数 ×整数 の学習 では ,数直線 や面積図 をもとに ,単位分数 に着目 させることで ,整数 ×整数 ,整数 ÷整数 の計算 に帰着 できることに 気付 かせる 。ここで ,次時 からの 問題解決 の



中1 一次方程式の分数は整数になおそう 中学数学の方程式 中間 期末テスト 高校入試対策




分数 整数 の掛け算 計算ドリル 問題集 数学fun




分数のかけ算の計算プリント 帯分数編 全240問無料 算数パラダイス




東大問題にもチャレンジ 分数が整数になる条件 オモワカ整数 18 全21回 数学専門塾met Note



分数取整数最值问题 西瓜视频搜索
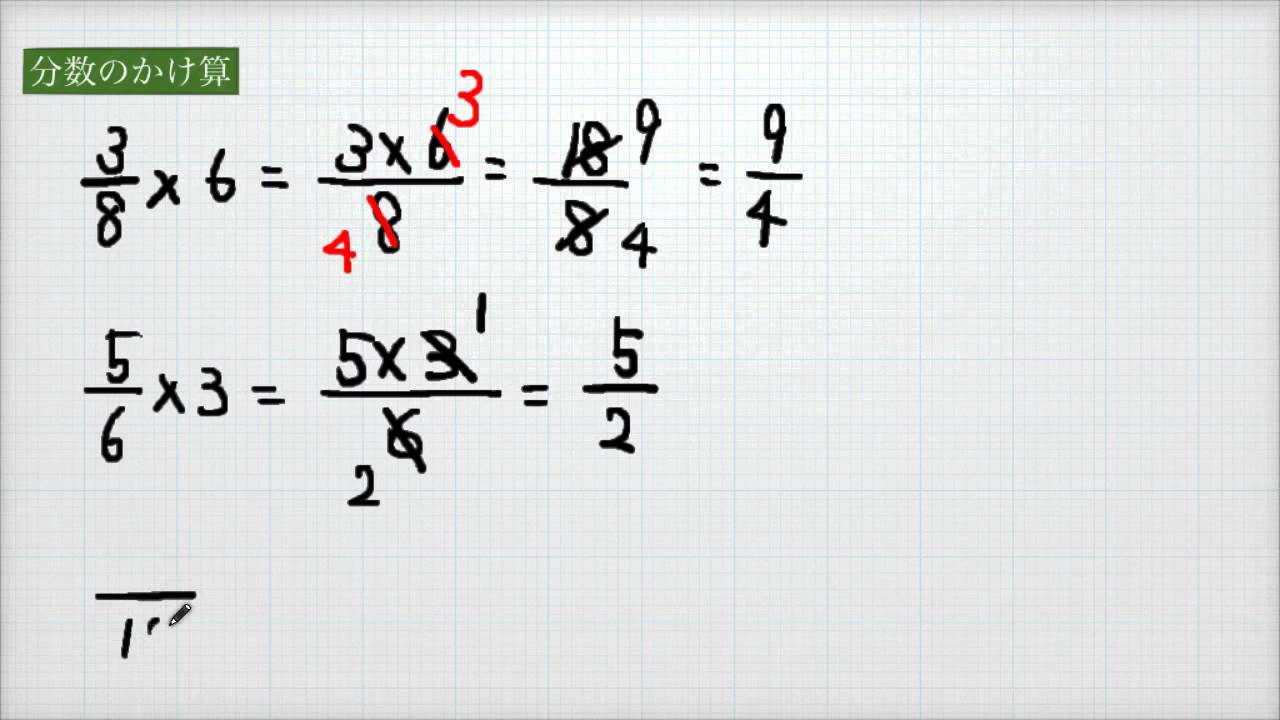



小学校5年 算数 分数のかけ算 分数に整数をかける 約分 Youtube




5年算数 分数のかけ算 分数 整数 を作成 おっくうの教材作成日記 楽天ブログ
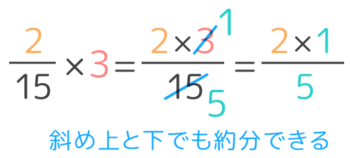



小学5年生 帯 真 分数と整数のかけ算 を図解 そうちゃ式 分かりやすい図解算数 別館
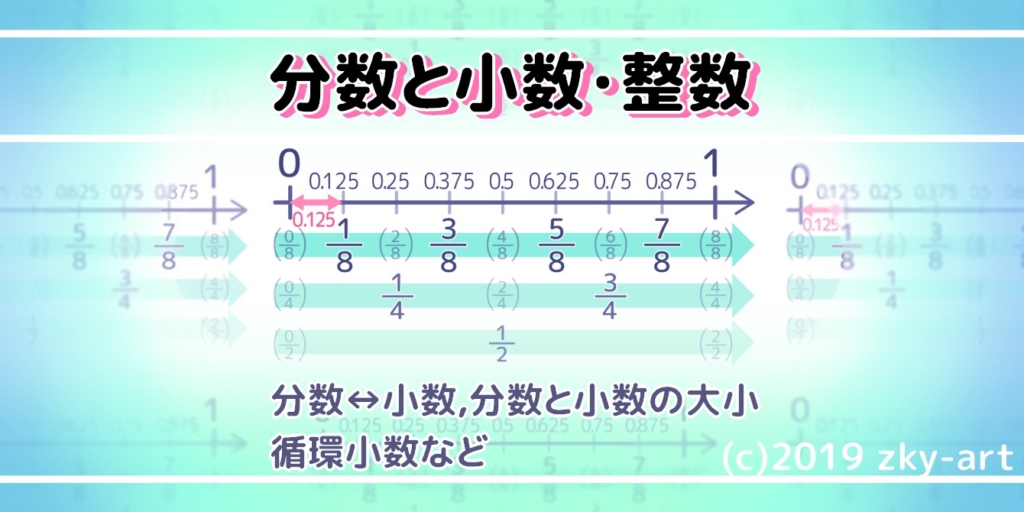



分数を 循環 小数で表す 整数に変換する方法 大小比較の練習問題もあり そうちゃ式 分かりやすい図解算数 別館



1




小学5年生の算数 動画 分数と小数 整数の関係 変身編の問題 19ch



早ね早おき朝5分ドリル 小6計算
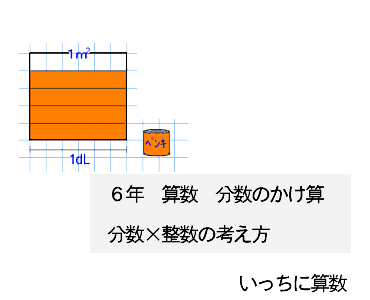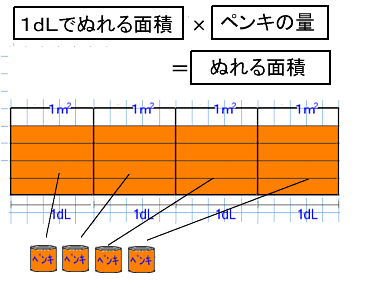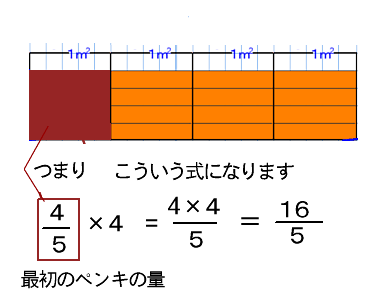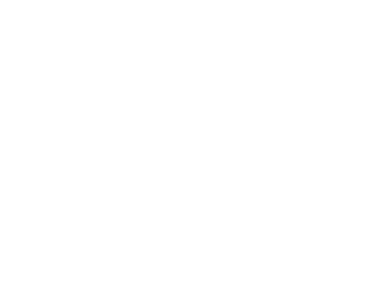



6年算数 分数 整数 分数 整数 教え方のポイント



分数 整数の求め方 教育考現学




分数のかけ算 分数と整数の積 積が整数 小6 学習プリント




小6算数 分数のかけ算 指導アイデア みんなの教育技術




5年生算数ドリル 分数 かけ算 わり算



Www Chofu Schools Jp Fujimidai Sho Documents 6sansua I Pdf



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料



Www Kumonshuppan Com Wpr Pdf Parts Pdf
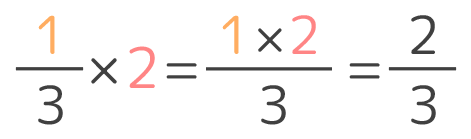



小学5年生 帯 真 分数と整数のかけ算 を図解 そうちゃ式 分かりやすい図解算数 別館




5年生算数ドリル 分数 かけ算 わり算



1
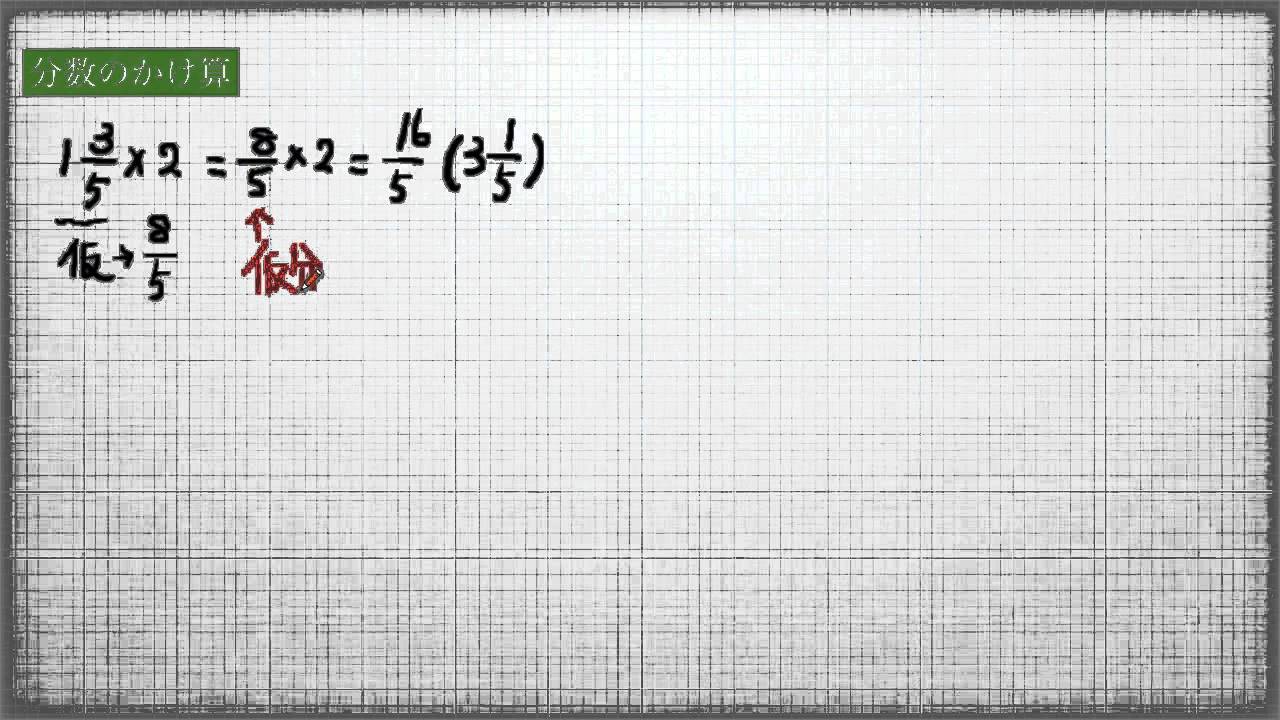



小学校5年 算数 分数のかけ算 帯分数 整数 Youtube




小5 算数 小5 29 分数と小数 整数の関係 変身編 Youtube



5年生の 分数 整数 のソフト さくら社



ドリルズ 小学6年生 算数 の無料学習プリントまとめ整数小数分数の文章題




分数形の不定方程式の解き方をイチから解説 数スタ
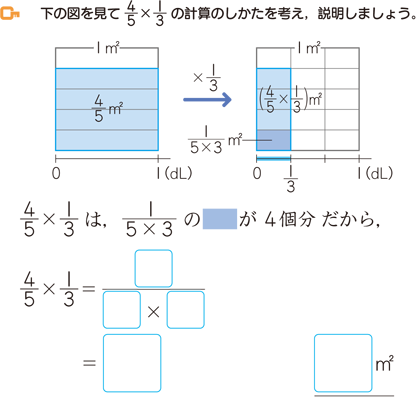



面積図 算数用語集




小学6年生の算数 分数と整数のかけ算 分数 整数 整数 分数 練習問題プリント ちびむすドリル 小学生




小学6年生の算数 分数 整数のかけ算 練習問題プリント ちびむすドリル 小学生
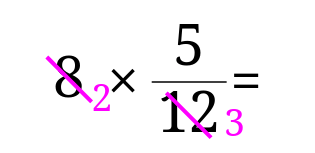



分数と整数の掛け算で約分があるときのやり方は どうやって説明する みけねこ小学校




世界一分かりやすい算数 小5 分数 1




6年生 分数の掛け算 まなび365 小学生の算数プリントを自動作成 無料で自宅学習



Uxmsnpnsrepa4m




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun
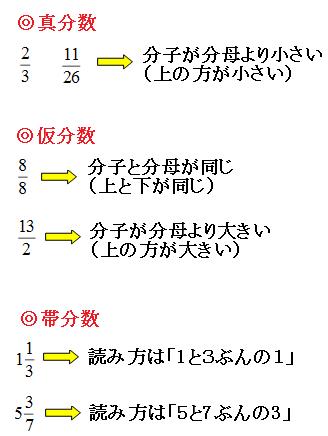



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利




分数と整数の足し算引き算が分からなくなってしまいました どなたか途中式や解説お願いい Clear




分数のかけ算 分数 整数 Youtube




分数と整数の足し算引き算が分からなくなってしまいました どなたか途中式や解説お願いい Clear




整数と分数の割り算について 整数と分数の割り算について教えてくださ 小学校 教えて Goo




分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note




怎么用整数减去分数 最有妙招网



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料




つまずきをなくす 小3 算数 計算 整数 小数 分数 単位 Amazon Com Books




小学5年生向け分数のかけ算問題



6年算数 分数 整数 分数 整数 教え方のポイント




怎么用整数减去分数 最有妙招网
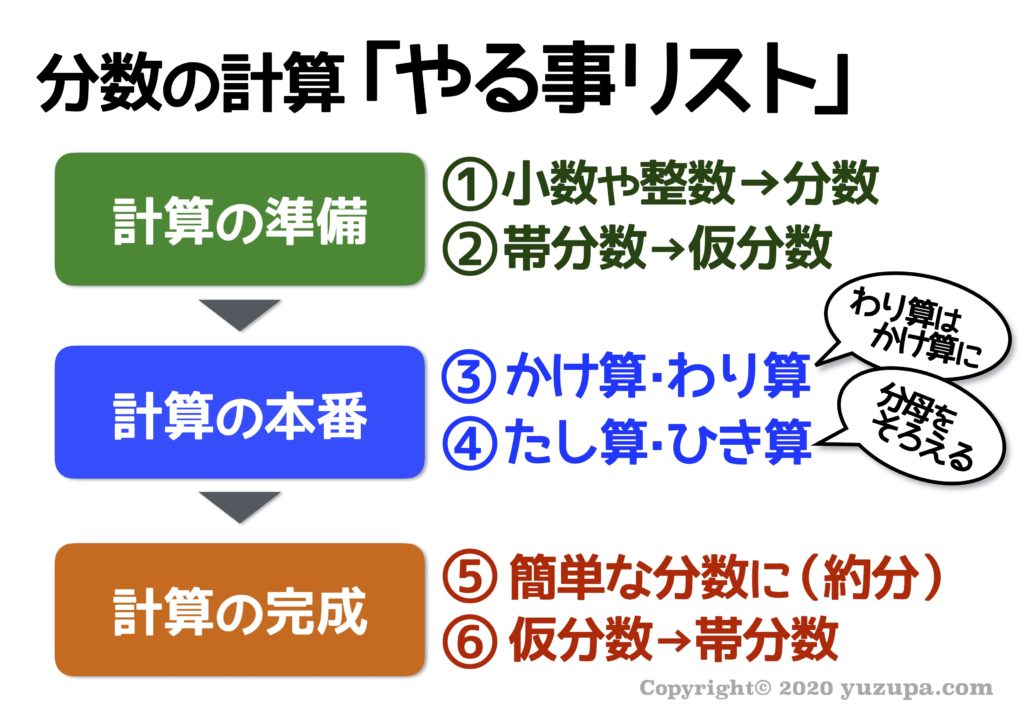



中学受験 分数の計算で間違え連発 やる事リスト で驚くほど上達 かるび勉強部屋
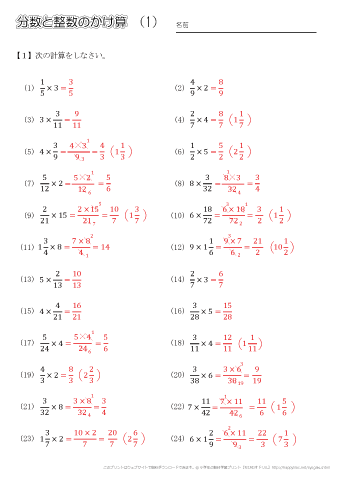



小学6年生の算数 分数と整数のかけ算 分数 整数 整数 分数 練習問題プリント ちびむすドリル 小学生




分数が整数になる条件 整数問題が面白いほどわかる Youtube
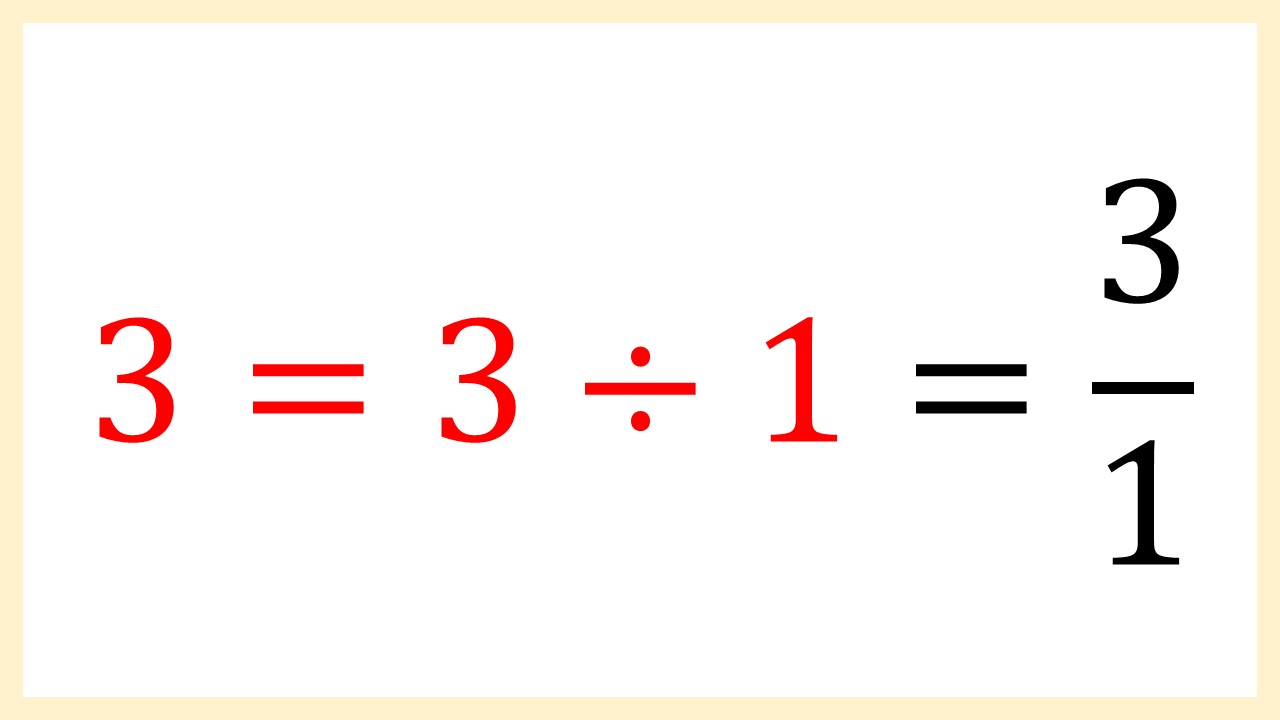



よくわかる 割り算を分数に直す方法 例題あり




整数問題 その1 入試に見る 単位分数 Online数学授業




有理数包含负数吗 有理数包括什么 三人行教育网 Www 3rxing Org




小学6年生 算数 無料問題集 逆数 おかわりドリル



分数取整数最值问题 西瓜视频搜索




小学校5年 算数 分数を小数や整数で表す Youtube




分数の文字式と整数の掛け算 よく使う非常に大切な知識 中学や高校の数学の計算問題



3




Dekirukodomo Com Wp Content Uploads 19 12 Img



11 有理数 無理数の問題 京極一樹の数学塾




高校数学b 整数mとnの間にある分母pの既約分数の和 受験の月




怎么用整数减去分数 最有妙招网



分数が分からない理由



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料




18 東大 数学 理系第2問解説 東大合格請負人 時田啓光 整数 C 整数 既約分数 東大合格 請負人の究極の学び方ブログ




連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト
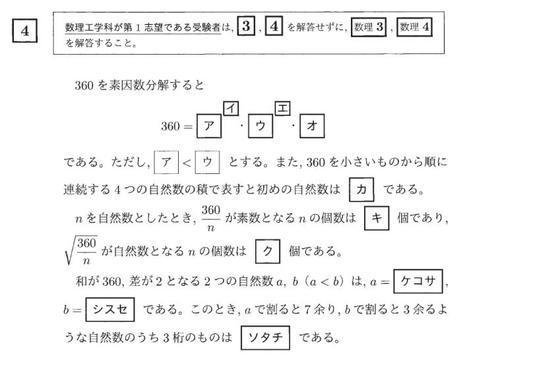



既約分数に関する整数問題です 大学入試数学問題の解説 解答
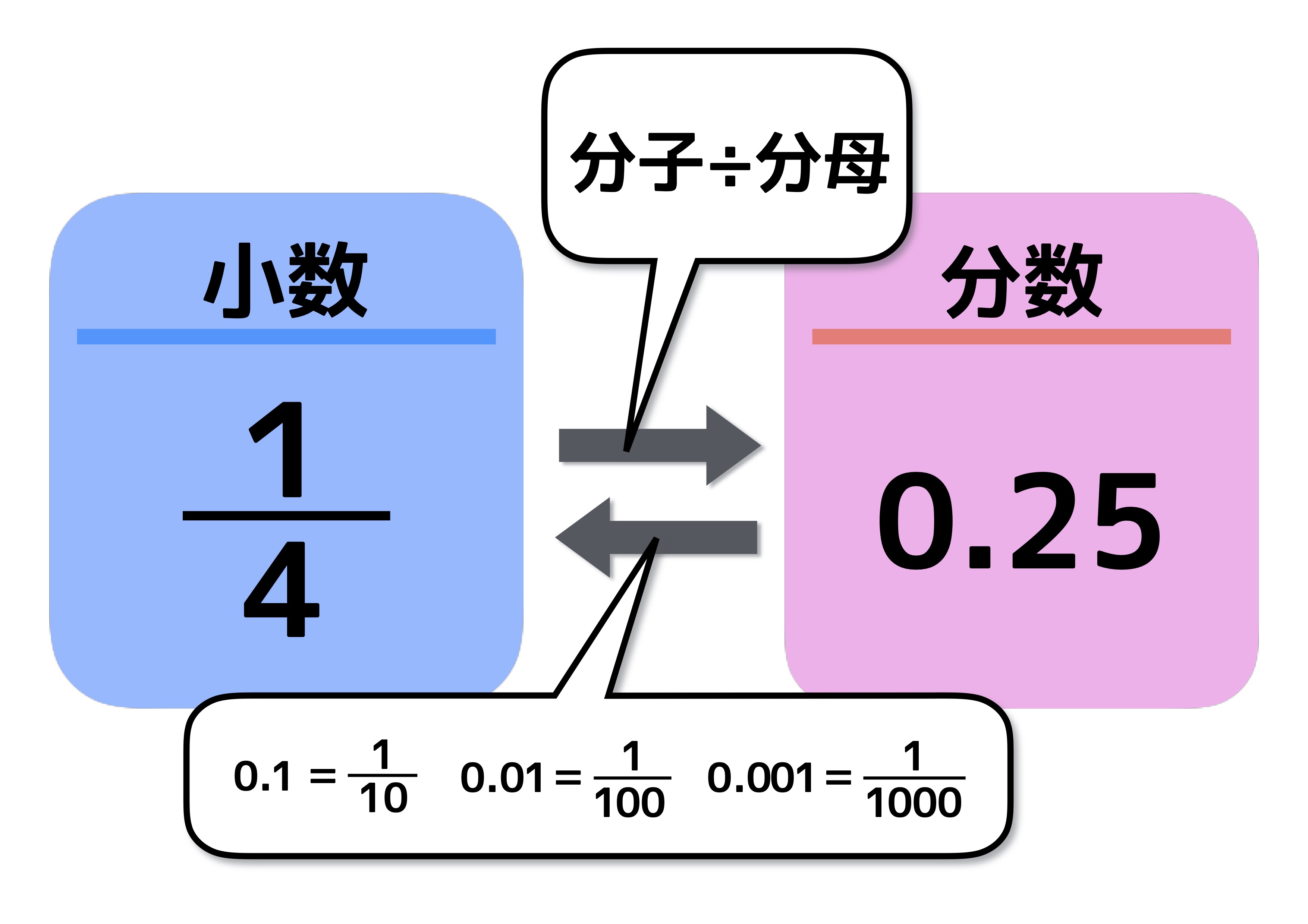



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料




分子与整数相乘 分数乘整数 用分数的分子与整数相乘的积作分子 分母不变 为什么分子要乘整数 的积作分子 而分母不变 三人行教育网 Www 3rxing Org



ドリルズ 小学5年生 算数 の無料学習プリント分数と整数のかけ算




分数 整数 の割り算 計算ドリル 問題集 数学fun




整数和分数加减法 整数和分数相加减怎么算 谢谢 三人行教育网 Www 3rxing Org




東大問題にもチャレンジ 分数が整数になる条件 オモワカ整数 18 全21回 数学専門塾met Note




分数を小数にするやり方 大人の学び直し算数 計算のやり方解説 無料




分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun
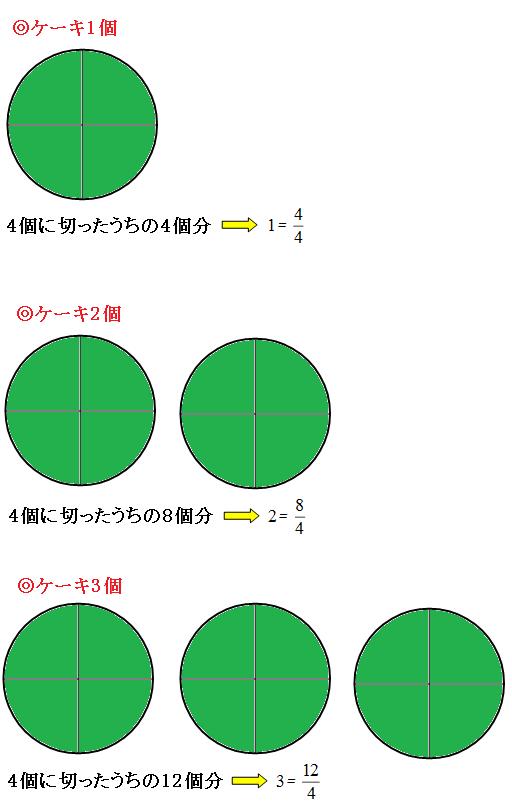



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利




小学6年生の算数 分数のわり算 分数 整数 整数 分数 練習問題プリント ちびむすドリル 小学生




帯分数の計算方法と仮分数への書き直し方
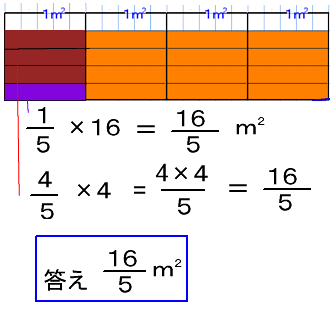



6年算数 分数 整数 分数 整数 教え方のポイント




小学5年生の算数 動画 分数と小数 整数の関係 比べる編の問題 等号と不等号 19ch
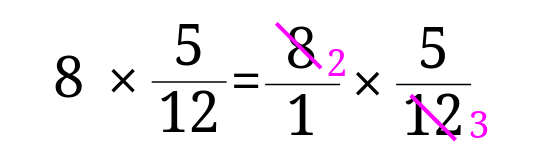



分数と整数の掛け算で約分があるときのやり方は どうやって説明する みけねこ小学校



分数の引き算 整数から




小5 算数 小5 30 2 分数と小数 整数の関係 Youtube



分数 整数の求め方 教育考現学



分数取整数最值问题 西瓜视频搜索



分数 整数 Youtube


